今回探求するのは、私たちの正体は仮想世界に生きるNPC、「ノンプレイヤーキャラクター」、すなわちゲームの中の人間なのか、という問題です。この話題はこれまで何度も取り上げてきましたが、今回は今までと違うアプローチ、つまり、推理や推測などで分析するのではなく、数学を使って、私たちが仮想現実に生きている確率を計算してみたいと思います。数学と聞いて難しく感じる方もいるかもしれませんが、今回使う数学は中学生でも理解できるものなので、安心してください。それでは、ぜひ最後までお付き合いくださいね。
仮想現実の数学的検証
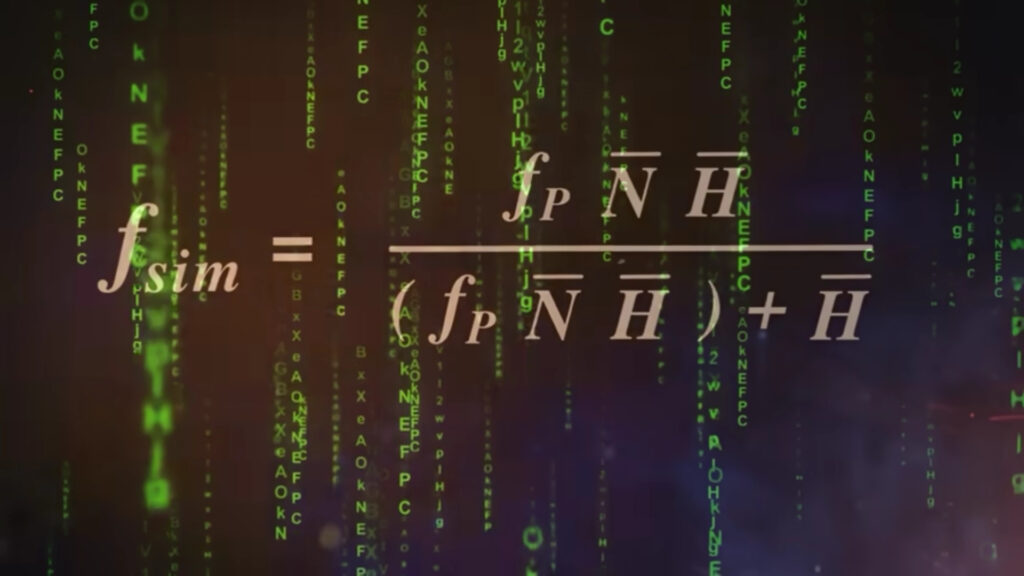
以前のシミュレーション仮説の動画でもお話ししましたが、オックスフォード大学の哲学者ニック・ボストロムは、厳密な数学的手法で、私たちがコンピュータのシミュレーションによる仮想現実に住んでいる確率を計算しました。その結果、限りなく1に近い数字(99.99999…%)が得られたのです。つまり、私たちは仮想世界に住んでおり、私たち一人ひとりがNPCであるのはほぼ確実であるという結論です。これはボストロムが示した数学の公式です。パッと見て全く意味が分からない、お手上げな気がしますが、その中身は中学レベルの数学で成り立っています。これから、誰にでも理解できるように順を追って説明していきます。
イーロン・マスクはとあるインタビューの中で、「この世界が現実である確率は十億分の一だ」と述べました。彼はこのように主張するとき、ボストロムが論文で示した理屈を引き合いに出しています。それはすなわち、次のようなロジックです。「理論上、コンピュータを使って私たちの生きている世界を丸ごとシミュレート可能なら、私たちはほぼ間違いなくコンピュータのシミュレーションによる仮想現実に生きている、ということになる」。論文の中で、ボストロムは厳密な数学的手法でこの仮説を論証しました。今から、ボストロムが導き出した数学的結論について、その過程を辿っていきましょう。
数学を学んだことのある人なら、数学的な推論を行うには、公理が必要だということを知っていると思います。公理というのは、議論の前提として置かれる仮定のことです。例えば、2本の平行線は永遠に交わることはない、というのは幾何学の公理の一つです。この公理は仮定であって、これに基づいて様々な定理や性質を考えることができます。難しく聞こえるかもしれませんが、実はこのようなことは日常生活の中にもあり、もっと簡単な例をあげるとしたら、「お金を払えば商品やサービスを受け取ることができる」というのは社会生活の基本的な前提として認識されています。この考えは、私たちがショッピングをする時やレストランで食事をする際の取引の基盤として存在しています。
同様に、ボストロムのシミュレーション仮説に関する推論にも、前提、もしくは公理が必要です。それは、「理論上、コンピュータは私たちが住んでいる世界と同じ規模と複雑さを持つ仮想世界をシミュレートすることができる」というものです。この公理の特筆すべきところは、そのような超越的なコンピュータを現実に作り出すことがどれほど難しいとしても、あくまで理論上、このレベルの仮想現実を作ることが可能であればよいという点です。しかし、これが本当に公理となりうるのでしょうか?そもそもこんな仮定は成り立たないのではないか、と疑問を呈する反対意見もあります。

私たちが住んでいる世界の複雑な物理法則をシミュレートするのは当然難しいですが、それが実現される可能性を丸っきり否定する根拠はそれほどありません。本当に問題となるのは、人間を含む生き物の「意識」をシミュレートすることです。理論上でも、人間などの生き物の意識をシミュレートすることは不可能であり、ボストロムが提唱した公理は成立しないというのがメジャーな反対意見の一つです。これに対するボストロムの解釈は、意識はひとつの機能にすぎず、神秘的で不可解なものではないという理解です。その機能は必ずしも人間の脳という素材のみで実現されるものではありません。同じ機能を実現するために、素材の選択肢は複数あります。
例えるならば、時間を正確に表示する機能を実現するために、機械式時計、電子時計、携帯電話、コンピュータなどなど、あらゆる選択肢が考えられるのです。それらはすべて、時間を表示する機能を私たちに提供できます。同じく、シリコンベースの素材であるコンピュータは、炭素ベースの素材である人間の脳とは素材が異なりますが、コンピュータの演算能力さえある程度強力ならば、適切なアルゴリズムを経て、完全に人間の脳と同じレベルの意識をシミュレートすることができます。
具体的に、人間の脳には非常に多くの神経細胞があり、これらの異なる神経細胞は互いに接続し、一種の神経回路網を形成していますが、コンピュータも演算能力の範囲でこのような神経回路網を完全にシミュレートすることができます。しかし、それだけで脳のはたらきを再現することに直結するわけではありません。人間の脳の神経回路網は非常に複雑で、脳内の神経細胞の数は1,000億近くもありますが、その一方、現在のコンピュータはおよそ1秒間に1億から1兆回の演算が可能というレベルです。人間の脳内の各神経細胞のシナプスと軸索の数のつながりを正確にシミュレートしようとする場合、必要な演算能力としてはおよそ1秒間に10の14乗から17乗回の演算が要求されます。現在のコンピュータの演算能力はこのレベルに遠く及びません。ただ、忘れてはならないのは、ボストロムの理論の前提、もしくは公理は、理論上、このレベルの演算能力を達成できればいいのだと強調している点です。
「ムーアの法則」というものがありますが、これは、半導体の技術が進化するにつれて、コンピュータの演算能力が約2年ごとに倍増するという法則です。今後もこの法則の通りに技術発展が望めるなら、100年後だろうが1万年後だろうが、いずれ人類は強力な演算能力を持つ超越的なスーパーコンピュータを作れるようになります。その時、コンピュータがシミュレートするNPCは、脳のはたらきと同じだけの現象を再現するに至っており、それはもはや自意識を持っていることと同義です。そして、自己意識を持つNPCをシミュレートすることが理論的に可能であるならば、その他の自然環境や宇宙環境のシミュレーションはもっと簡単に思えます。
これに対し、環境をシミュレートするのは人間の脳をシミュレートするよりも難しいという指摘もあります。特に、ミクロスケールの環境をシミュレートする場合、例えば電子の動きをシミュレートするには多くの演算回数が必要です。しかし、これはボストロムの議論にとって問題ではありません。結局、すべては演算能力の問題であり、演算能力さえ十分に強力であれば、理論的には我々が生きている世界をシミュレートできると言えてしまうからです。ですので、ボストロムの提唱した公理が理論的に成立するならば、いずれそれが現実になる可能性があります。

ボストロムは、人間世界をシミュレートできるレベルの演算能力まで発達したそのような人類文明を、ポスト・ヒューマン文明と呼んでいます。
それでは、ここからいよいよ数学的計算へと議論を進めましょう。ここでいう数学的計算というのは、確率を導こうとする計算を意味します。つまり、私たち一人ひとりが、コンピュータによってシミュレートされた世界に住む確率、もしくは、私たちがNPCである確率はどれほどあるのかを計算するものです。
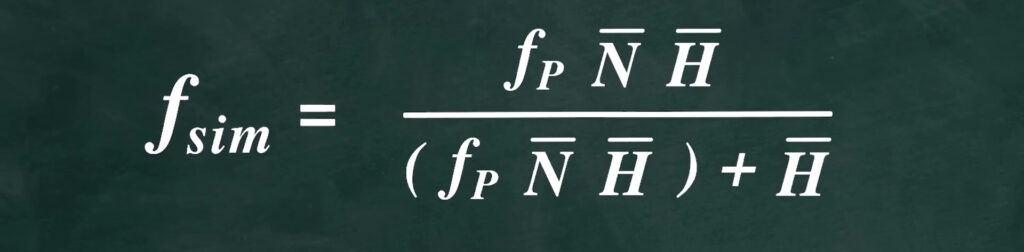
この確率はf simで表わされます。f simが意味しているのは、すべての自己意識を持つ観察者のうち、コンピュータのシミュレーションによる仮想現実に住むNPCである人の割合です。難しく聞こえるかもしれませんが、つまり、私たちは「現実世界に生きている人間である」、もしくは「仮想現実に生きているNPCである」、真実はこの2つのどちらかであるため、NPCの人口をNPC人口プラス本当の人間の人口で割った値は、私たちがNPCである確率となります(f sim=NPC人口/NPC人口+本当の人間の人口)。ここで付け加えておきたいのは、「本当の人間の人口」とは、生きている人の数だけでなく、亡くなった人の数も含まれるということです。その舞台が地球だとすると、既存の70億人の人口だけでなく、死亡した人々も含めて、本当の人間の人口の合計は約1000億人です。同様に、ここで言う「NPC人口」は、現在オンラインのNPCの数だけでなく、オフラインになったNPCの数もカウントされます。
それでは式に戻って計算の過程を見ていきましょう。分子の「NPC人口」は、人類文明がポスト・ヒューマン文明まで生き延びる確率fp、かける、ポスト・ヒューマン文明が生み出した仮想現実の数N、かける、各仮想現実にいる人口H、で得られる値です。したがって、式は最終的にはこのような形になります。f sim=NPC人口/NPC人口+本当の人間の人口=fp x N x H/ (fp x N x H)+H。

理解しやすくするために、それぞれの記号の意味をさらに詳しく説明します。fpは人類文明がポスト・ヒューマン文明まで生き延びる確率と説明しましたが、厳密には、すべての文明のうち、ポスト・ヒューマン段階まで生き残った文明の割合を示しています。想定される将来として、人類の技術が仮想文明をシミュレートできるレベルまで発展できない可能性もあるし、その前に人類文明が滅亡する可能性もあります。そのため、計算式には、人類文明がポスト・ヒューマン文明の段階まで発展できるかどうかという確率を加味します。
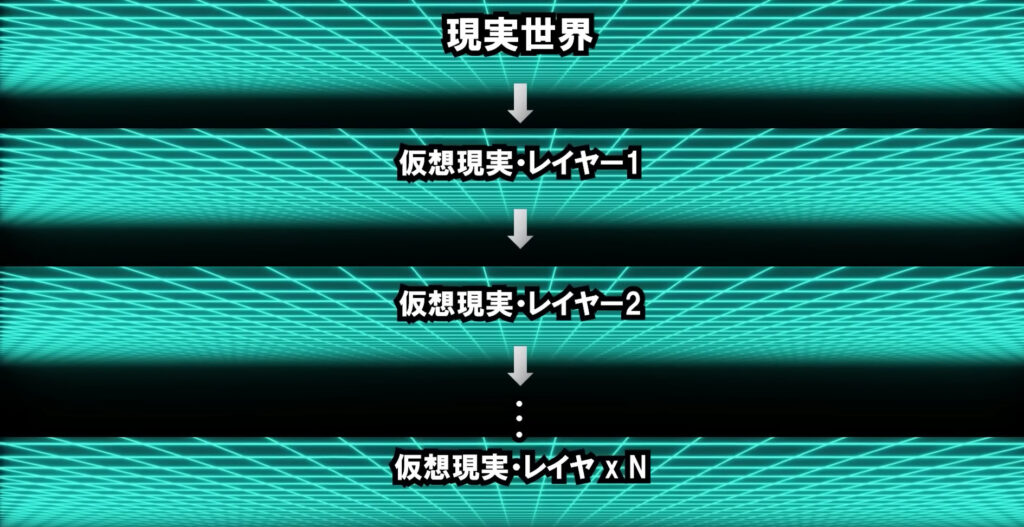
Nは、文明がポスト・ヒューマン文明の段階に入った後、その文明が平均していくつの仮想現実を作るかを示す値です。なぜ平均なのか?その理由は、ポスト・ヒューマン文明が1つのパターンしかないとは限らないからです。さらに、ポスト・ヒューマン文明が、コンピュータを使って仮想現実の文明をシミュレートした後、その仮想現実にいる文明がポスト・ヒューマン文明の段階に発展したとき、彼らもまたその世界の中で仮想現実を作るかもしれません。このように、仮想現実の数はどんどん増えていきます。イメージしてみてください。現実世界の文明を最上階だとしたら、その文明が仮想現実を一旦作ると、その仮想現実もまた彼らの世界にとっての仮想現実を作るかもしれません。これが繰り返され、下層に向けて仮想現実が次々と作られていき、無限に巨大化するピラミッド構造、ないしは木構造が生まれます。このような展開は重大な事態をもたらす可能性があると指摘する人もいます。すなわち、下層にある仮想現実が増えるにつれ、最上層のコンピュータ、つまり最上階の現実世界にあるコンピュータの負荷が大きくなりすぎて、クラッシュしてしまうかもしれないというリスクです。ただし、これは大した問題ではないとボストロムは反論しています。仮にコンピュータがダウンしたとしても、現実の世界にはまだほかにも数多くのコンピュータがあり、それらのコンピュータによる仮想現実もほぼ無数にあるため、数字的な影響はほぼゼロだと言えるからです。以上がNの説明です。次はHの意味を説明しましょう。
先ほど、Hは各仮想現実にいる人口だと説明しましたが、式を見て違和感を覚えた方もいるのではないでしょうか。厳密には、Hは現実世界に生きている人口を根本的には表しています。ですので、分母に加えられている本当の人間の人口は、Hで表わされます。しかし、分子の「NPCの人口」を導く計算にも同じHをかけており、一見これは計算式として破綻しているようにも思われるかもしれませんが、NPC人口の算出にもHが必要である理由は、ポスト・ヒューマン文明が自分たちの文明をシミュレートした仮想世界を開発するのなら、自分たちの文明の人口を参照する可能性が高いからです。あらためてこれらの要素を落とし込んだ計算を確認すると、分子の「NPCの人口」は、文明がポスト・ヒューマン文明の段階まで発展できる確率fp、かける、ポスト・ヒューマン文明が生み出した仮想現実の数N、かける、各仮想現実にいる人口数H、で得られた値となります。ここまでで、式の意味についてはすべて解説しました。完全に理解していただくために、少し冗長になっているかもしれませんが、この式のロジックが実はシンプルなものであることをご理解いただけたのではないでしょうか。では次に、この式で得られた結果、つまり私たちが仮想現実にいるNPCである確率はどれくらいなのかを実際に計算していきましょう。
中学校の数学知識で式を解いてみると、Hが約分されるので、式はこのような形になります。f sim=fp x N/(fp x N)+1。ただし、もうひとつ考慮すべき要素は、仮想現実を開発する意欲の有無です。つまり、ポスト・ヒューマン文明で現実世界をシミュレートする能力を持つまでに文明が発展したとしても、その文明は必ずしも世界をシミュレートする意欲を持っているわけではありません。倫理的あるいは法的な理由から、ポスト・ヒューマン文明は自意識のあるNPCが存在する仮想世界を開発することをきんじられているのかもしれないし、また、今は想像もつかない何らかの理由で、開発が禁止される可能性もあります。
したがって、仮想世界を開発する意志を持つポスト・ヒューマン文明の割合を示すfiを設定する必要があります。この要素を式に取り込むと、式はこのようになります。f sim=fp x fi x Ni/(fp x fi x Ni)+1。fiは、仮想現実を開発する意欲のあるポスト・ヒューマン文明の割合、Niは、仮想世界を開発する意志を持ったポスト・ヒューマン文明が開発する仮想世界の平均数を表します。さて、結局のところこの式をどのように解読すればよいのでしょうか?
ボストロムが思うには、1つだけでも仮想現実を作ろうとするポスト・ヒューマン文明があれば、Niが膨大な値になります。その理由は私たちの文明を見れば察することができます。私たちの文明では、コンピュータ・ゲームを作る能力があり、かつてそれが禁じられておらず、人々はゲームを作る意欲もあります。このような文明の中で、ゲームが1つしか開発されていないということはあり得ません。百歩譲って、その文明が1つの仮想現実しか開発していないとしても、先ほどお話しした通り、仮想現実は下層に向けてどんどん増えていきます。その結果、ほぼ無数の仮想現実が誕生することになるのです。したがって、この式にあるNiという値は、宿命的に、非常に大きい数字を示すことになります。これでようやく式の結果を導くことができます。Niは非常に大きい値なので、分母に加えられた1はほとんど機能せず、分子と分母はほぼ等しくなります。つまり、f simはほぼ1に等しい、99.999999...%ということになります。これで、私たちが仮想世界に住むNPCである確率は、99.999999...%になるという結論が得られました。
考察
では、本当にボストロムが主張するように、私たちは本当に血肉の通わないNPCなのでしょうか?ここからは僕の個人的な意見となります。ボストロムの主張が正しいのであれば、最上層の現実世界が存在するはずです。私たちが最上部の現実世界に住む現実の人間である可能性は確かにありますが、問題は、無数にある世界の中で私たちの世界が唯一の現実世界に該当するという確率は極めて低く、イーロン・マスクが言った十億分の一どころではなく望み薄だということです。ただし、式に戻ってよく考えると、別の可能性も見出せます。それは、fpが限りなく0に近い場合、もしくはfiが限りなく0に近い場合です。この2つのパターンを考えてみると、分母に加えられた1が機能するようになり、式の結果も0に近い値になります。こうなれば、話は丸っきり逆転して、私たちが仮想現実にいるNPCである可能性は0に近くなります。では、fpが限りなく0に近い場合、あるいはfiが限りなく0に近い場合、それらはそれぞれどのような状況を意味しているのでしょうか?

まず、fpが限りなく0に近いことが意味するのは、ほぼすべての文明がポスト・ヒューマン文明に発展する前に絶滅したということ。そして、fiが限りなく0に近いことが意味するのは、文明はポスト・ヒューマン文明にまで発展できるものの、ほぼすべてのポスト・ヒューマン文明が、仮想現実の開発に消極的だということ。この2つの想定がどれほどの確率なのかは何とも言えませんが、もしこれらの条件が望めないのであれば、私たちはNPCであることになります。すなわち、人類が仮想現実を作れるまで技術力を発展させ、同時に仮想現実を作る意欲もある場合、私たちが今生きているこの世界は仮想現実であり、私たちはNPCであるということになります。
動画の最後に、次のようなシーンを想像してみましょう。数百年後、人類のコンピュータの演算レベルは飛躍的な進歩を遂げ、ゲーム会社は現実世界のシミュレーションゲームの開発に成功しました。そのゲームは非常にリアルで、ゲーム内のすべてのNPCは、自己意識を持ち、現実の人間と区別がつきません。人々は科学技術の発展に歓声を上げ、みんながゲームをダウンロードしてこの未知の体験に胸を弾ませます。しかし、しばらくすると人々は感じ始めます。「これは未知の体験などではないのではないか?」
“胡蝶の夢”、夢の中で蝶になってひらひらと飛んでいたら、ふと目を覚まします。しかし、あまりに鮮明なそれは、自分が蝶になった夢を見ていたのか、蝶こそが本来の自分で、今いる自分は蝶が見ている夢なのではないか、そんな疑問を投げかけます。そして、仮想現実を生み出したシミュレーションゲームは、さらなる問いをあなたに突きつけるのです。「すべてが夢なのではないか?」と。
それでは、今日もありがとうございました。






コメント